About
-
Currently, I am a Research Scientist at INRIA Bordeaux working on Efficient Training of Neural Networks, previously I was at Skoltech with laboratories of Prof. Ivan Oseledets and Prof. Andrzej Cichocki.
-
I received my Ph.D. in Probability Theory and Statistics and Master’s in Mathematics from Lomonosov Moscow State University, and in parallel, I completed a Master’s-level program in Computer Science and Data Analysis from the Yandex School of data analysis.
-
My previous research deals with Compression and Inference Speed-up of computer vision models (classification/object detection/segmentation), Neural Ordinary Differential Equations (Neural ODEs), as well as neural networks analysis using low-rank methods, such as tensor decompositions and active subspaces. Also, I had some audio-related activity, particularly, I participated in the project on speech synthesis and voice conversion. Some of my earlier projects were related to medical data processing (EEG, ECG) and included human disease detection, artifact removal, and weariness detection.
-
Research interests: Efficient Training and Inference of Neural Networks, Model Compression, Tensor Decompositions for DL, Neural ODEs, Robustness, Transfer Learning, Hyper Networks, Interpretability of DL.
Selected publications
Efficient Training of Neural Networks
Survey on Efficient Training of Large Neural Networks
IJCAI-ECAI 2022
Modern Deep Neural Networks (DNNs) require significant memory to store weight, activations, and other intermediate tensors during training. Hence, many models don’t fit one GPU device or can be trained using only a small per-GPU batch size. This survey provides a systematic overview of the ap- proaches that enable more efficient DNNs training. We analyze techniques that save memory and make good use of computation and communication re- sources on architectures with a single or several GPUs. We summarize the main categories of strate- gies and compare strategies within and across cate- gories. Along with approaches proposed in the lit- erature, we discuss available implementations.
HiRemate: Hierarchical Approach for Efficient Re-materialization of Neural Networks
ICML 2025
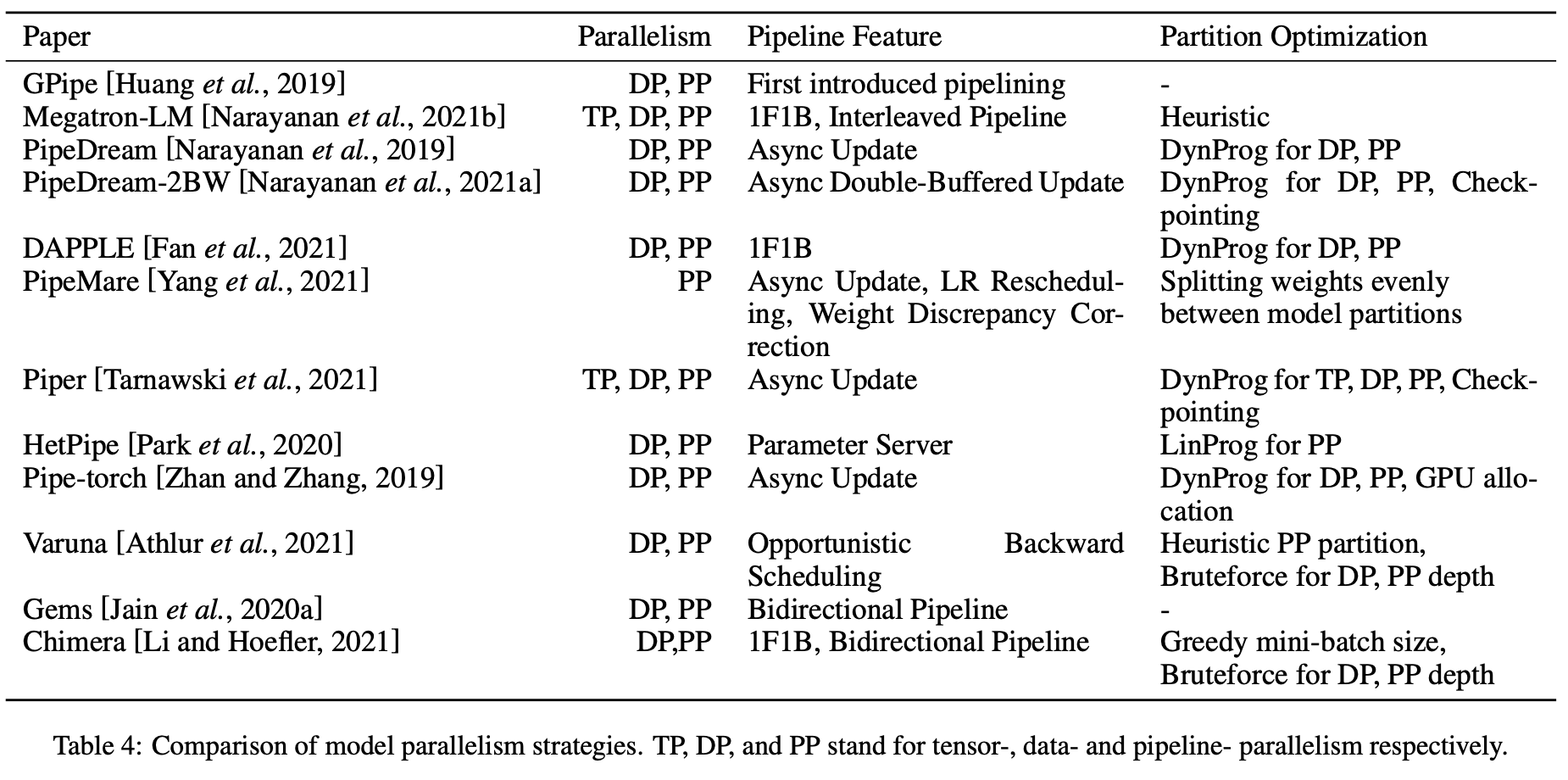
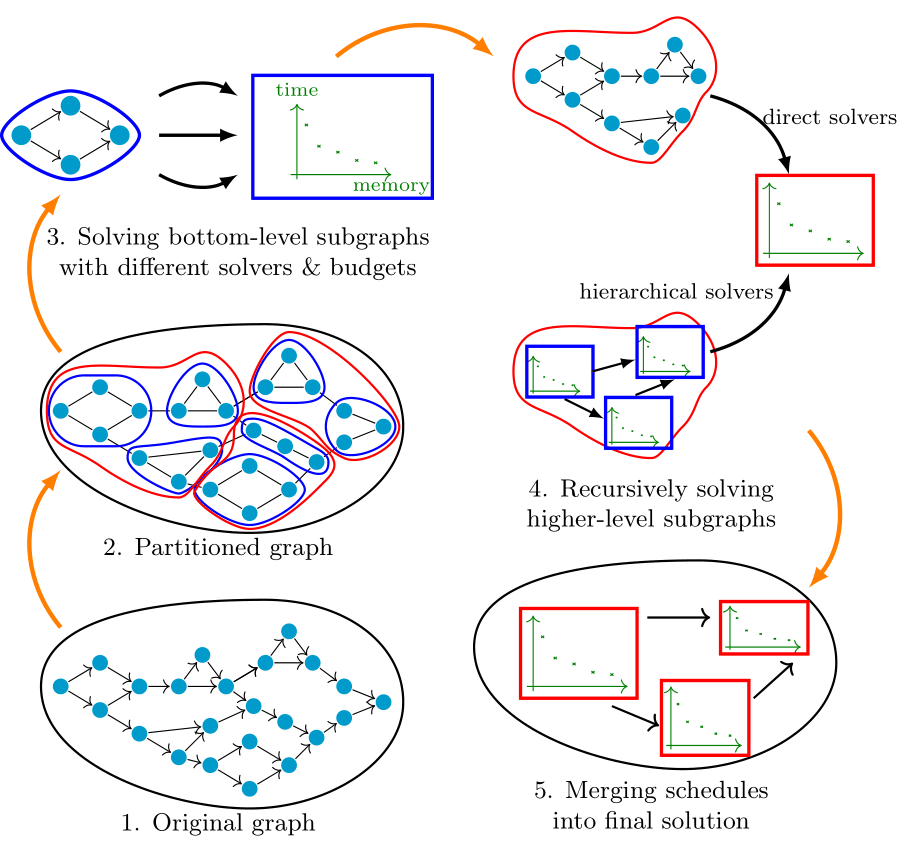
Training deep neural networks (DNNs) on memory-limited GPUs is challenging, as storing intermediate activations often exceeds available memory. Re-materialization, a technique that preserves exact computations, addresses this by selectively recomputing activations instead of storing them. However, existing methods either fail to scale, lack generality, or introduce excessive execution overhead. We introduce HiRemate a hierarchical re-materialization framework that recursively partitions large computation graphs, applies optimized solvers at multiple levels, and merges solutions into a global efficient training schedule. This enables scalability to significantly larger graphs than prior ILP-based methods while keeping runtime overhead low. Designed for single-GPU models and activation re-materialization, HiRemate extends the feasibility of training networks with thousands of graph nodes, surpassing prior methods in both efficiency and scalability. Experiments on various types of networks yield up to 50-70% memory reduction with only 10-15% overhead, closely matching optimal solutions while significantly reducing solver time.
Few-bit backward: Quantized gradients of activation functions for memory footprint reduction
ICML 2023
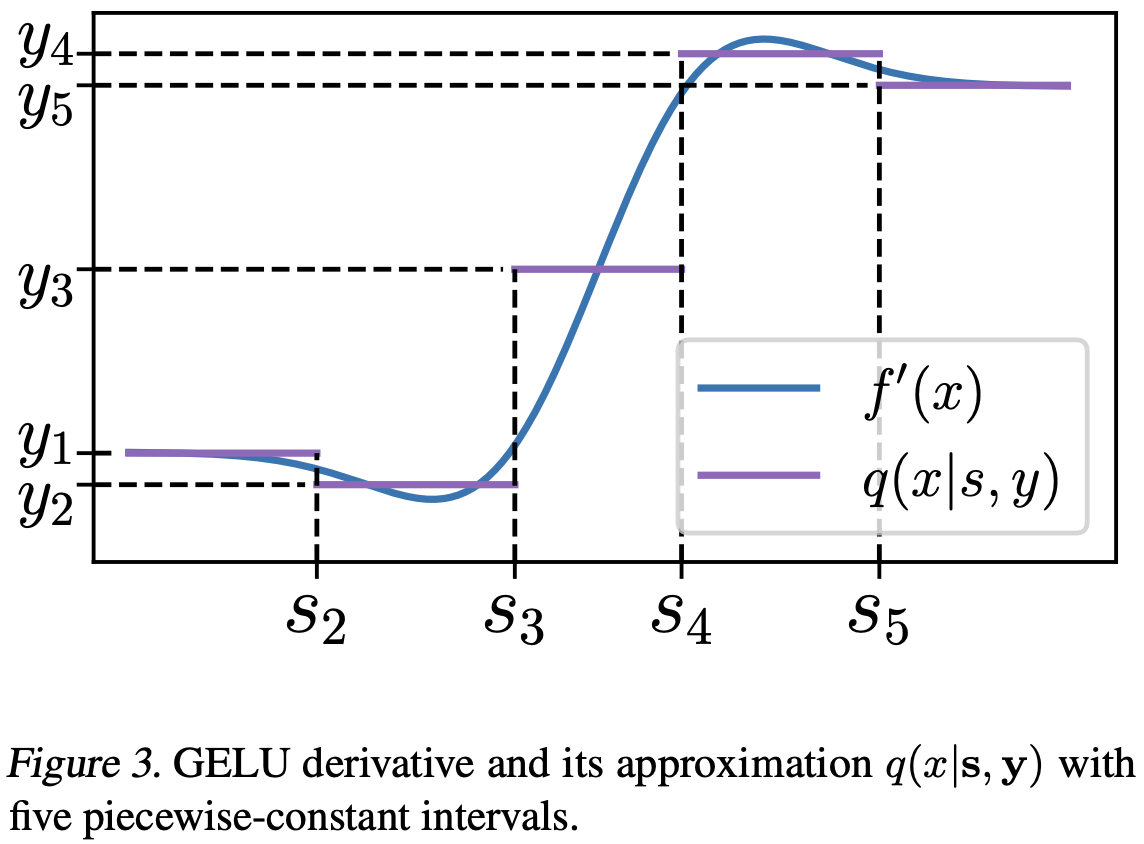
Memory footprint is one of the main limiting factors for large neural network training. In backpropagation, one needs to store the input to each operation in the computational graph. Every modern neural network model has quite a few pointwise nonlinearities in its architecture, and such operations induce additional memory costs that, as we show, can be significantly reduced by quantization of the gradients. We propose a systematic approach to compute optimal quantization of the retained gradients of the pointwise nonlinear functions with only a few bits per each element. We show that such approximation can be achieved by computing an optimal piecewise-constant approximation of the derivative of the activation function, which can be done by dynamic programming. The drop-in replacements are implemented for all popular nonlinearities and can be used in any existing pipeline. We confirm the memory reduction and the same convergence on several open benchmarks.
Inference Speed-up and Compression of Neural Networks
Quantization Aware Factorization for Deep Neural Network Compression
Journal of Artificial Intelligence Research, 2024
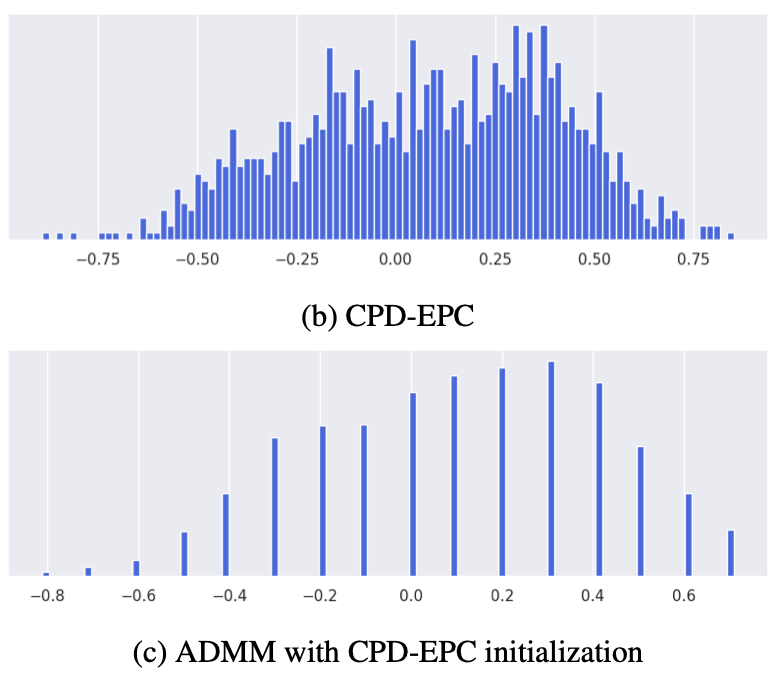
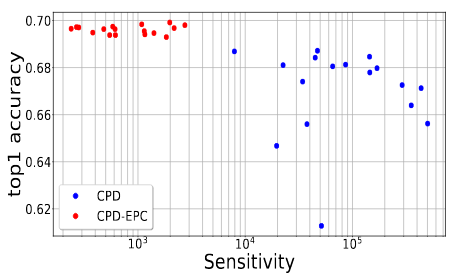
Tensor decomposition of convolutional and fully-connected layers is an effective way to reduce parameters and FLOP in neural networks. Due to memory and power consumption limitations of mobile or embedded devices, the quantization step is usually necessary when pre-trained models are deployed. A conventional post-training quantization approach applied to networks with decomposed weights yields a drop in accuracy. This motivated us to develop an algorithm that finds tensor approximation directly with quantized factors and thus benefit from both compression techniques while keeping the prediction quality of the model. Namely, we propose to use Alternating Direction Method of Multipliers (ADMM) for Canonical Polyadic (CP) decomposition with factors whose elements lie on a specified quantization grid. We compress neural network weights with a devised algorithm and evaluate it's prediction quality and performance. We compare our approach to state-of-the-art post-training quantization methods and demonstrate competitive results and high flexibility in achiving a desirable quality-performance tradeoff.
Stable Low-rank Tensor Decomposition for Compression of Convolutional Neural Network
ECCV 2020
Most state of the art deep neural networks are overparameterized and exhibit a high computational cost. A straightforward approach to this problem is to replace convolutional kernels with its low-rank tensor approximations, whereas the Canonical Polyadic tensor Decomposition is one of the most suited models. However, fitting the convolutional tensors by numerical optimization algorithms often encounters diverging components, i.e., extremely large rank-one tensors but canceling each other. Such degeneracy often causes the non-interpretable result and numerical instability for the neural network fine-tuning. This paper is the first study on degeneracy in the tensor decomposition of convolutional kernels. We present a novel method, which can stabilize the low-rank approximation of convolutional kernels and ensure efficient compression while preserving the high-quality performance of the neural networks. We evaluate our approach on popular CNN architectures for image classification and show that our method results in much lower accuracy degradation and provides consistent performance.
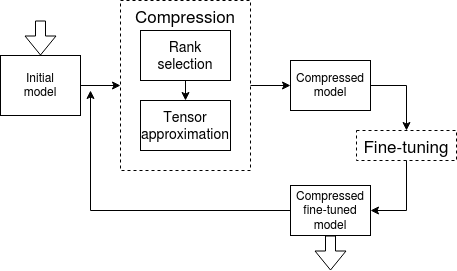
Automated Multi-Stage Compression of Neural Networks
ICCV 2019 Workshop on Low-Power Computer Vision
We propose a new simple and efficient iterative approach for compression of deep neural networks, which alternates low-rank factorization with smart rank selection and fine-tuning. We demonstrate the efficiency of our method comparing to non-iterative ones. Our approach improves the compression rate while maintaining the accuracy for a variety of computer vision tasks.
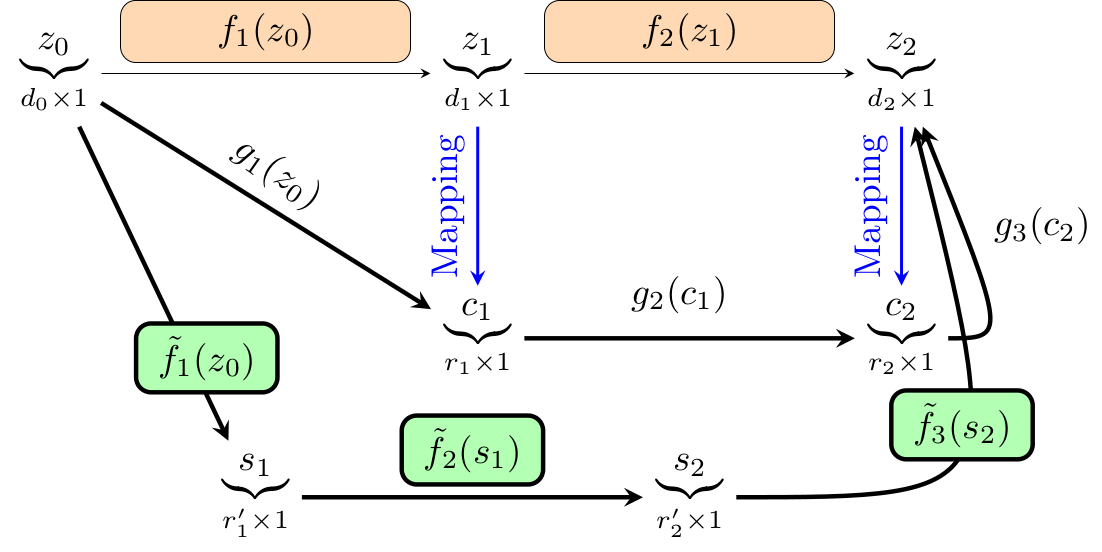
Reduced-Order Modeling of Deep Neural Networks
Computational Mathematics and Mathematical Physics Journal, 2021
We introduce a new method for speeding up the inference of deep neural networks. It is somewhat inspired by the reduced-order modeling techniques for dynamical systems. The cornerstone of the proposed method is the maximum volume algorithm. We demonstrate efficiency on VGG and ResNet architectures pre-trained on different datasets. We show that in many practical cases it is possible to replace convolutional layers with much smaller fully-connected layers with a relatively small drop in accuracy.
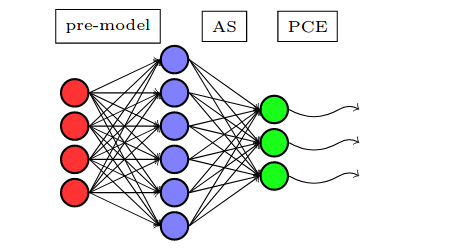
Active Subspace of Neural Networks: Structural Analysis and Universal Attacks
SIAM Journal on Mathematics of Data Science (SIMODS), 2020
Active subspace is a model reduction method widely used in the uncertainty quantification community. Firstly, we employ the active subspace to measure the number of" active neurons" at each intermediate layer and reduce the number of neurons from several thousands to several dozens, yielding to a new compact network. Secondly, we propose analyzing the vulnerability of a neural network using active subspace and finding an additive universal adversarial attack vector that can misclassify a dataset with a high probability.
Neural Ordinary Differential Equations (Neural ODEs)
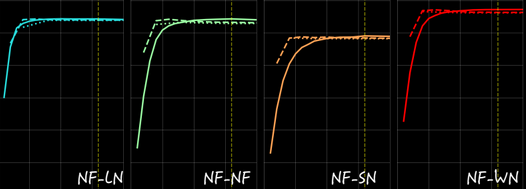
Towards Understanding Normalization in Neural ODEs
ICLR 2020 DeepDiffeq workshop
Normalization is an important and vastly investigated technique in deep learning. However, its role for Ordinary Differential Equation based networks (neural ODEs) is still poorly understood. This paper investigates how different normalization techniques affect the performance of neural ODEs. Particularly, we show that it is possible to achieve 93% accuracy in the CIFAR-10 classification task, and to the best of our knowledge, this is the highest reported accuracy among neural ODEs tested on this problem.
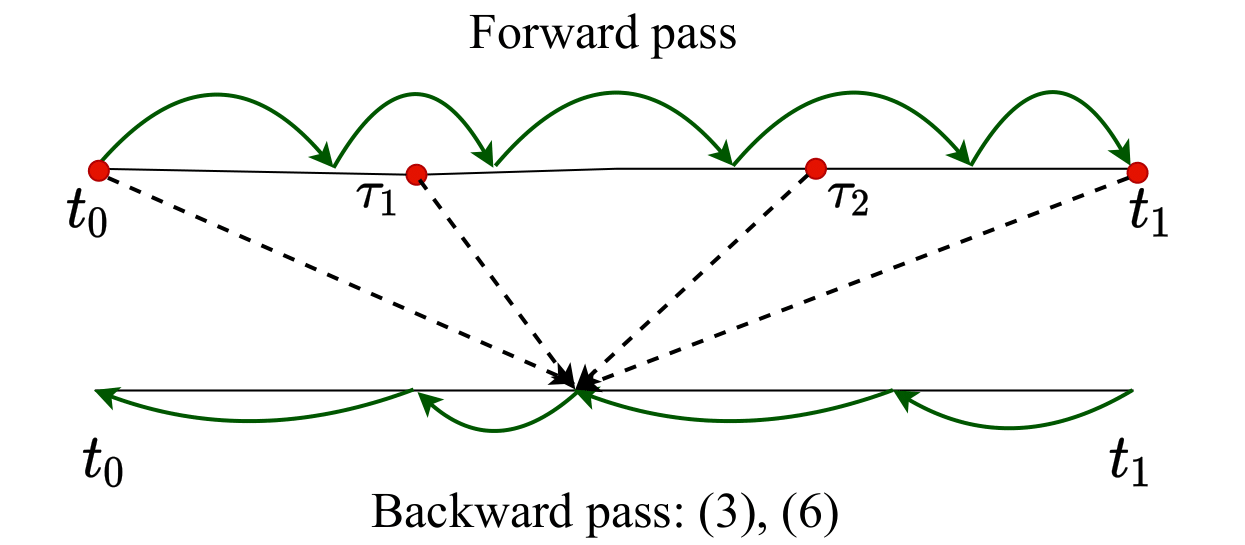
Interpolation technique to speed up gradients propagation in neural ordinary differential equations
NeurIPS 2020
We propose a simple interpolation-based method for the efficient approximation of gradients in neural ODE models. We compare it with reverse dynamic method (known in literature as ''adjoint method'') to train neural ODEs on classification, density estimation and inference approximation tasks. We also propose a theoretical justification of our approach using logarithmic norm formalism. As a result, our method allows faster model training than reverse dynamic method on several standard benchmarks.
Selected projects

MetaSolver
A Python library that supports neural ODEs with MetaODE blocks: propagation through them is performed using sampling or ensembling of ODE solvers rather than a pre-defined one.
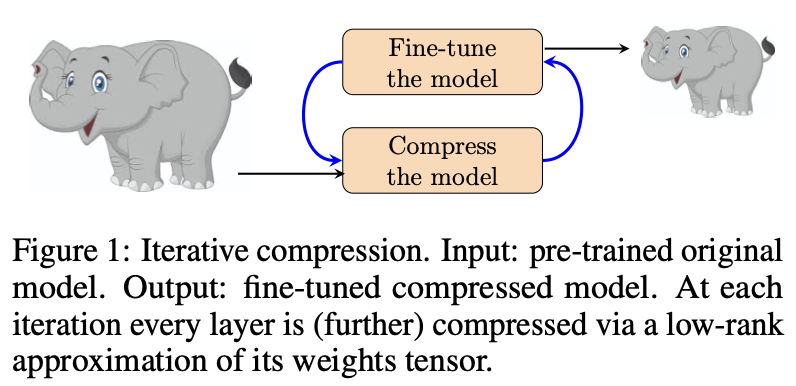
MUSCO: MUlti-Stage COmpression of neural networks
A Python library for convenient neural network compression based on tensor approximations. It supports both automated and manual compression schemes.

FlopCo: FLOP and other statistics COunter for Pytorch neural networks
A Python library FlopCo has been created to make FLOP and MAC counting simple and accessible for Pytorch neural networks. Moreover, FlopCo allows to collect other useful model statistics, such as number of parameters, shapes of layer inputs/outputs, etc.

Data loaders for speech and audio data sets
A Python library with PyTorch and TFRecords data loaders for convenient preprocessing of popular speech, music and environmental sound data sets.
Speaker identification using neural network models
In the framework of this project a WaveNet-style autoencoder model for audio synthesis and a neural network for environment sounds classification have been adopted to solve speaker identification task.